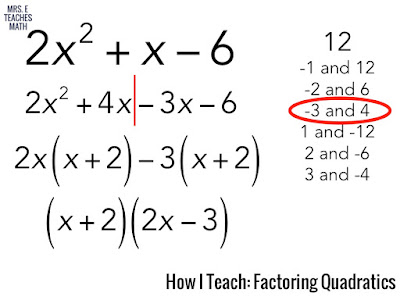I know of a few different methods people use to teach factoring, but I’ve never been a fan of the “fancy” methods. They just don’t work for me. When I teach factoring, I actually teach the unit backward. I teach factoring by grouping, factoring trinomials when a≠1, factoring trinomials when a=1, then special cases.
I start with factoring by grouping, because once students can do that, factoring trinomials is easy. I tend to spend an extra day teaching factoring by grouping. When students have that down, I move on to factoring trinomials. I prefer teaching when a≠1 first, because when a=1 is really just a special case. If students can handle the “harder” version, there almost isn’t a need to teach the “easier” version.
So, this is how I teach factoring. This is not revolutionary. It is not new, or even interesting. But it works, every time. I've often heard this method called "splitting the middle".
First, I have students multiply the “a” value by the “c” value.
Then, I tell them they are looking for two numbers that multiply to that value. I have them make a list.
Only after that do I have them find the pair of numbers that adds to the “b” value.
Next, I have students split the middle and finish by factoring by grouping. So, example student work for the example would look like this:
I prefer to teach factoring this way because it doesn’t rely on tricks and it works every time. Also, after this lesson, teaching a=1 is just a special case.
In my TpT store, I have a full unit with activities to teach polynomials and factoring. The unit includes guided notes, worksheets, warm-ups, activities, and other materials to effectively teach your students. Click to find my Polynomials and Factoring Unit.

In my TpT store, I have a full unit with activities to teach polynomials and factoring. The unit includes guided notes, worksheets, warm-ups, activities, and other materials to effectively teach your students. Click to find my Polynomials and Factoring Unit.